Program „Dyfrakcja”
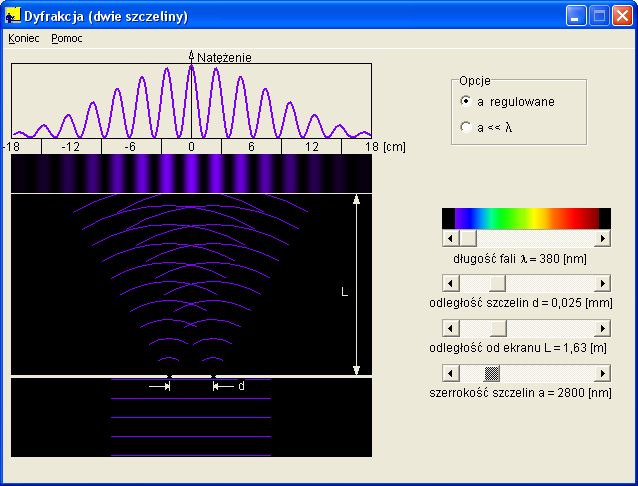
Program pozwala obserwować wynik równoczesnej dyfrakcji i interferencji fal świetlnych powstałych w wyniku przejścia płaskiej fali świetlnej przez przesłonę z dwoma szczelinami. Dla szczelin o skończonej szerokości (nie punktowych) w wyniku interferencji fal otrzymujemy obraz, w którym natężenia prążków nie są stałe (jak w doświadczeniu Younga) ale zależne od obrazu dyfrakcyjnego pojedyńczej szczeliny.
Natężenie światła w obrazie interferencyjnym dla dwóch
punktowych szczelin opisane jest równaniem: Iint = I0cos2b, gdzie b = pdsinq/l, przy czym d jest odległością między szczelinami, l długością fali świetlnej, a q kątem pod jakim światło dociera ze szczelin do danego punktu P ekranu (ustawionego za szczelinami).
Natomiast natężenie fali ugiętej na szczelinie jest dane równaniem: Idyfr. = I0(sina/a)2, gdzie a = pasinq/l, przy czym a jest szerokością szczeliny.
Łączny efekt możemy teraz otrzymać zastępując w równaniu dla obrazu interferencyjnego stałą amplitudę (przypadek szczelin punktowych) realnym natężeniem dyfrakcyjnym (szczeliny o skończonej szerokości). Otrzymujemy wtedy równanie: I = I0cos2b(sina/a)2
Ten wynik opisuje następujące fakty: 1) W pewnym punkcie ekranu natężenie światła, z każdej szczeliny osobno, jest dane przez obraz dyfrakcyjny tej szczeliny; 2) Obrazy dyfrakcyjne dwóch szczelin rozpatrywanych oddzielnie nakładają się (fale interferują). Otrzymany obraz jest więc iloczynem czynnika interferencyjnego i dyfrakcyjnego.
W programie można za pomocą odpowiednich suwaków zmieniać szerokość szczelin a, ich wzajemną odległość d, odległość szczelin od ekranu L oraz długość fali l i obserwować jak obraz dyfrakcyjny zależy od tych parametrów.
Więcej na temat dyfrakcji możesz dowiedzieć się z Notatek do Wykładów z Fizyki (Wykład 29) dostępnych na stronie internetowej http://galaxy.uci.agh.edu.pl/~kakol/ - niestety strona już nie działa.
Uruchom bez instalacji po rozpakowaniu.
Zrzut
Pobierz program Dyfrakcja dyfrakcja.zip (pobrań: 1742)
Tadeusz Rokicki
Ostatnia modyfikacja: 6-06-2025 , 11:01
Ostatnia wizyta: 08:47:02
14 listopada 2025